First, a concave lens is one which is thinner in the center than it is near the edges. This is shown in this diagram:
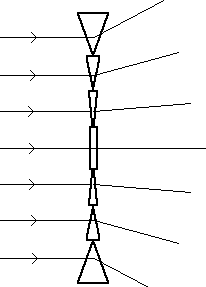
When we look at the cross-section of a concave lens we notice that the edges resemble prisms. In fact, a stack of prisms of varying angles can be used to simulate the actions of a concave lens. One such is shown here and is called a Fresnel Lens.
Light passing through the angled prisms near the edges is bent significantly while light passing through the flat, central area is hardly bent at all. Light rays which are parallel to one another when approaching such an arrangement are spread out becoming diverging as shown here:
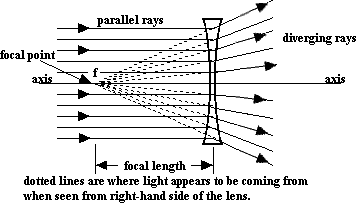
We start with this general pattern to define the focal point for our concave lens.
DEFINITION 1:
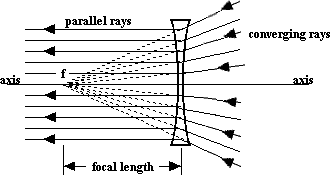
The focal point of a concave lens is the point where light rays parallel to the axis seem to diverge from after passing through the lens. The distance from the lens to this point is called the focal length of the lens.
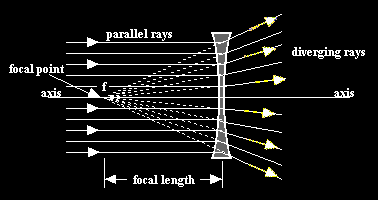
Because it seems rather odd to represent light as a dark line on a white page, the diagram above has been inverted below to show white light on a black background. The principle is the same.
Now the question is where one would find parallel light rays in nature? How common or uncommon are parallel light rays if most of the light we seen on a daily basis is diverging to one degree or another?
If an object is very far away, the angle formed between adjacent light rays is very small. Depending on the focal length of the specific lens, this distance might be anywhere from a few meters to a kilometer. If the object is very far, say 93,000,000 miles (1.5 x 1011 m) like the Sun, the distance is sufficiently far that light rays are essentially parallel. So sunlight is a convenient source of parallel light rays. Objects that are a great distance away like hills or trees also furnish rays that are almost parallel. Finally, lasers are a relatively inexpensive source of parallel light due to their inherent nature.
NOTE: The light rays do not actually originate from the focal point. Rather, their behavior on the other side of the lens is such that they appear to be coming from there. Remember that the original light rays were parallel to the axis!
NOTE 2: In the diagrams above, light rays are shown bending at the center of the lens. This is a construction technique and is used only for convenience. In fact the rays would bend once upon entering the lens and a second time upon exiting.
BOTTOM LINE: If we see a light ray that's parallel to the axis of a concave lens we know where it is going to go on the other side -- it will diverge as if it had started at the focal point.
DEFINITION 2:
Converging light rays striking a concave lens but headed towards a point on the other side can be bent until they emerge parallel to the axis. The point that causes this to happen is called the focal point.
Or as before, white light on a black background:
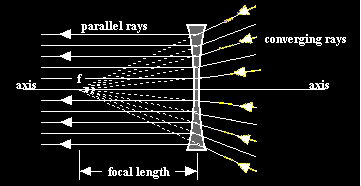
NOTE: Because we have defined "focal point" so precisely, we can understand that a light ray that is not parallel to the axis will not diverge from the focal point on the other side of the lens. Also we know that a light ray that does not head towards the focal point will not emerge parallel to the axis.
BIG NOTE:
A concave lens has two focal points - one on each side. They are equal distances from the lens. The lens does not have to have the same curvature on both sides for this to be true, and it doesn't depend on the direction the light takes entering the lens. It is the combined curvature that determines the focal point.
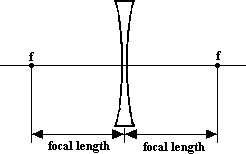
BIGGER NOTE:
Because no light actually goes through the focal point of a concave lens, it isn't "real" like the focal point of a convex lens. Light is never focused there but only appears to come from the focal point. The focal point of a concave lens is called "virtual" which means that it only appears to have the effect of a focal point.
When we purchase a concave lens, we specify the focal length with a negative number such as f = -5 cm. When the mathematics of image formation for concave lenses is worked out, it requires that we use a negative number for the focal length to get a correct answer.
HOW TO FIND THE FOCAL POINT:
If you wish to find the focal point of a concave lens, you could take it outside on a clear day. Allow the sunlight to pass through the lens and observe the pattern formed on a screen that is parallel to the axis and located at the center of the lens. IMPORTANT: Make sure the sunlight is aimed along the axis of the lens.
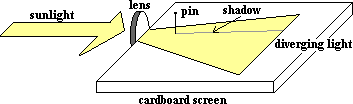
The pattern of light on the opposite side of the lens will be diverging. Trace at least two rays. You can place two pins in the path of the light and trace their shadows. Project these two paths back to where they intersect. This is the focal point. Remember, originally parallel rays diverge as if coming from the focal point.