BUILD UP:
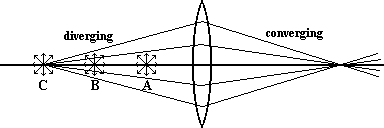
In the diagram below, we place a point light source at three different places along the axis of our convex lens. The locations are labeled A, B and C. Note that each of the sources would be sending light rays out in all directions.
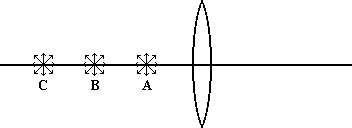
Now from position A, the light rays diverge with some striking the lens and passing through it. On the other side, we notice that the rays are still spreading out, they are still diverging. But we notice that they aren't diverging as much as before.
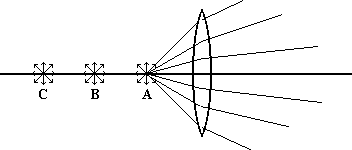
Perhaps at point B the light rays that strike the lens emerge parallel to one another on the opposite side as illustrated here.
We recognize this as exactly the condition described as focal point, with B being the focal point of our lens.
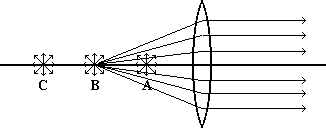
From position C, however, the light rays that strike the lens come together on the other side of the lens, or converge as shown here.
There is a unique place on the other side of the lens that the light rays converge. If we were to put a screen of some sort there, we would see a point of light. If the screen were now moved away from the lens, the light rays would begin to diverge and the light would spread out as if all the rays had come from that point, not from point C. And if our eyes were somewhat beyond the right-hand point to allow our lenses to focus correctly, we would see a point source of light at that location.
What would happen if we defined other points, the same distance from the lens as C, but above or below the axis? See the setup below, followed by the result.
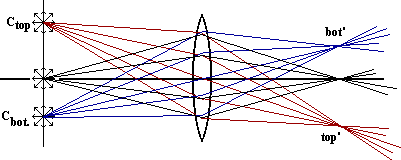
Notice how the light rays from the bottom converge to a point above the axis while the rays from above the axis converge to a point below the axis. Ctop represents the top of an extended light source, the place where light rays that started there come back together is the point labeled top', while Cbot represents the bottom of an extended light source. The place where these rays are converged is represented by bot'. In the diagram which follows, we overlay an arrow with its base at Cbot and its tip at Ctop. Light from every point on this object arrow would converge to a corresponding point in the line between bot' and top'.
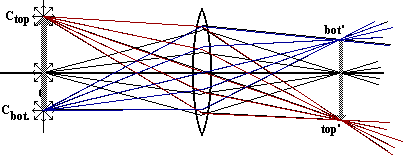
We have been able to reconstruct all of the rays which originally started at the object and passed through the lens. This reconstruction is the real image of the original object. A screen placed at that location would have a pattern on it that closely resembles the original object - the real image.
Not only were we able to reconstruct a pattern of light rays that resembles the original pattern, but once they have been brought together, the rays continue on out from there as if there were a real object at that point.
But the pattern is upside down. With a little visualization, you can imagine that the original arrow is rotated about the axis and is now pointing into the paper. How will the image point? Yes, out of the paper. The orientation of the image is both upside down relative to the original object and reversed right-to-left. Such an orientation is called inverted. The real image formed by a convex les is inverted.
SIZE:
If you observe closely, you will notice that the length of the object arrow in our diagram is slightly greater than the length of the image arrow. There must be some sort of size relationship which we must account for in any theory we develop.
PRINCIPLE RAYS:

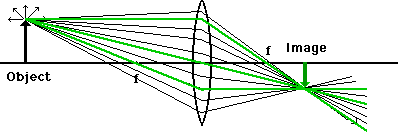
In this drawing we see any number of light rays, the red ones coming from the head of the object arrow and the blue ones coming from the tail. Even with only five rays coming from each point you can imagine how difficult it's going to be to calculate what direction to take each light ray after it strikes the lens. And to think that light does this automatically!
There are two light rays that we have a good idea about based on our definition of focal point. Even though all the rays will behave in a similar manner, we can use them to show us the general pattern.
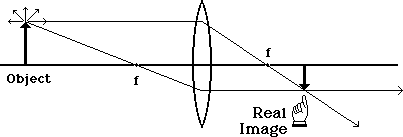
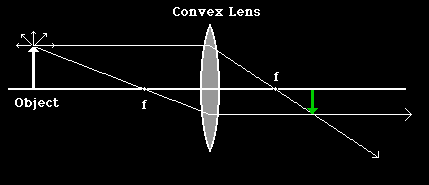
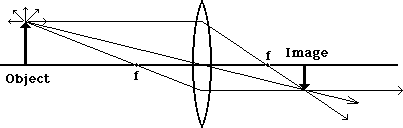
In the diagrams below, we concentrate our attention on the light coming from the tip of the object arrow. Note that we've now marked the locations of the focal points, one on each side of the lens, with the letter f.
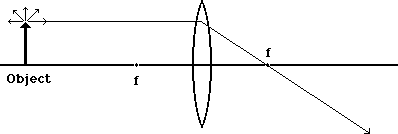
Of all the light rays, the one which started out parallel to the axis will pass through the lens and be bent towards the focal point on the other side. It doesn't stop there but goes on until it runs into something new.
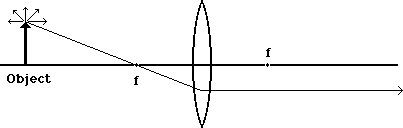
A light ray which goes through the first focal point will be bent until it emerges parallel to the axis. This is the complementary behavior to the previous one. Note that we know this behavior, while we can only approximate the behavior of other light rays.
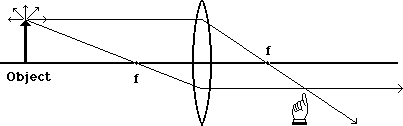
With both of these rays drawn, we see that they intersect at a particular place on the other side of the lens. Now if we had many more rays in our diagram, where would they intersect?
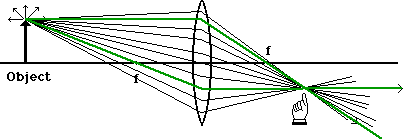
They all intersect at the same point. We don't need all of them to locate that point, but once we've located it, we can be assured that the rest will follow. So we can use just the two rays to locate the point and we call these the principle rays - the one that was originally parallel to the axis and the one which passed through the focal point.
The light from the center of the object will converge at the same distance on the other side of the lens, but will be closer to the axis. The light from the bottom of the object will likewise be the same distance, but will focus on the axis. If we join these points and draw in a complete image, we get the diagram below:
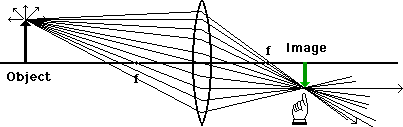
A screen placed at this location will show an entire image that looks remarkably like the original object, but it is inverted. But we only need the three principle rays to make the same conclusion about size and location shown here:
Things look slightly different, but better, when we see white light against a black background:
ANOTHER PRINCIPLE RAY:
When we consider a lens, we note that the sides of the lens near the center are approximately parallel. Thus light would behave very much like going through a piece of glass. In this diagram we remind ourselves about the path that light would take through a fairly thick piece of glass:
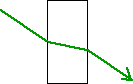
The light ray that emerges on the other side of the glass is parallel to the one which entered. It is displaced somewhat, but is going in the same general direction.
If the glass is thin, the displacement is minor. If it is thin enough, the displacement can essentially be ignored and we can approximate the path as simply a straight line. This approximation is often referred to as the thin lens approximation.

If our lens is thin - its thickness is small compared to the diameter, or thin compared to the distance between the object and the lens - we can see a ray going virtually straight through the center and then passing through the corresponding point on the image. This is shown here as a third principle ray.
OR
We mostly use the first two rays, the one parallel to the axis and the one that passes through the focal point, to determine the image location. This third ray will also arrive at the same point, but is dependent on an approximation to be as accurate as the others.
SUMMARY TO DATE:
- An object placed fairly far from a convex lens will form a
real image on the other side of the lens.
- The real image will be inverted - upside down and backwards
right to left.
- The real image can be formed onto a screen like in a slide
projector.
- The real image may be a different size than the object.
SIGNS:
For lenses, we develop a sense of signs in our mathematics. It comes from the direction that light travels through the lens. In the diagram which follows, note that the positive sense of things occurs when light starts on one side and converges on the other.
|
Object distance is positive |
Object distance is negative (very rare) |
|
Image distance is negative |
Image distance is positive |
|
Focal point is negative |
Focal point is positive |
Now we move on to take a look at the mathematics (geometry) of the real image. This is an important area and you should study it carefully.