BUILD UP:
In the diagram below, we place a point light source at three different places along the axis of our convex lens. The locations are labeled A, B and C. Note that each of the sources would be sending light rays out in all directions.
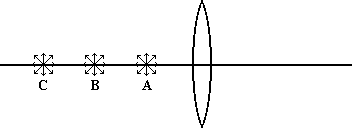
Perhaps at point B the light rays that strike the lens emerge parallel to one another on the opposite side as illustrated here.
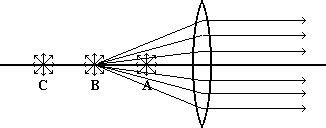
We recognize this as exactly the condition described as focal point, with B being the focal point of our lens.
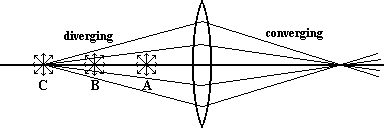
From position C the light rays that strike the lens come together on the other side of the lens, or converge as shown here.
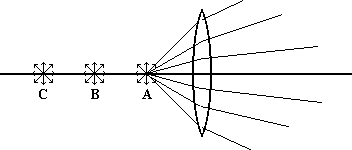
However, when light rays diverge from position A and strike the lens, the rays are still spreading out after passing through the lens. But we notice that they don't diverge as much as before. It is this behavior that leads to a new kind of image called virtual.
FORMING IMAGES:
We start out by placing an object at a distance that is less than the focal length from the lens. This is illustrated here:
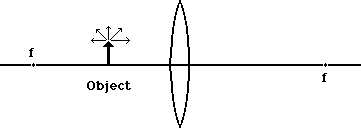
As before and as shown above, we consider the tip of our object arrow first. It sends light rays out in all directions, some of which goes through the lens. Of all the light which goes through the lens, we know definitely what happens to two of the light rays, and have a good idea about a third.
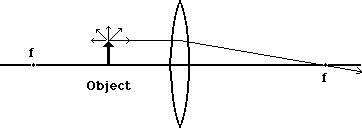
As shown here, the light ray that started at the object's tip and was parallel to the axis will be bent until it goes through the focal point on the other side of the lens.
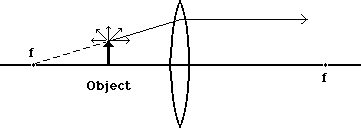
The light ray from the object which looks like it came from the focal point on the near side (see dotted line in the diagram) is bent until it goes parallel to the axis. Now if we put both of those rays onto the same diagram, we get the following:
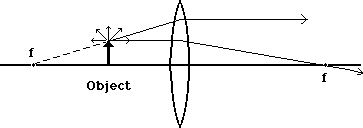
Now these two light rays don't meet. They came from the same place, but will never get together using this lens. When we look at them coming out of the lens, however, we can project backwards to a common place that both share, behind the lens, which is the place that both rays seem to be coming from.
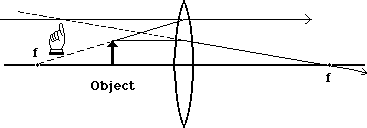
So when we see these two rays seeming to come from this point, we actually see all of the rays that go through the lens as if they came from the same point. This is illustrated here:
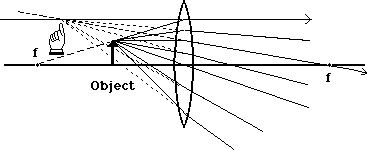
So this point would be where we would see the tip of the arrow. It follows that other points on the image of the arrow would lie below that point, ultimately forming the image shown here:
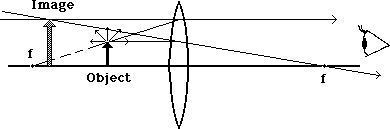
The image formed is upright, not inverted. It is enlarged from the size of the object. And it is further away from the observer thanthe original object. It is not formed by the convergence of light rays, but rather from the apparent source of the rays. Thus we refer to it as a virtual image rather than a real image.
APPLICATIONS:
Several important uses can be made from this set of characteristics. First, if we put an object between the lens and the focal point ("inside the focal point" is the way we usually describe this position) we will obtain an enlarged image. The most common use for such a lens used in this way is as a magnifying glass.
It would be ironic if a magnifying glass were to invert the image. We'd have to hold the object we're trying to inspect upside down!
One of the characteristics of the image is that it winds up further from us than the original object. This is an advantage, even if there were no magnification, in that we need to get objects far enough from our eyes that our lens system can focus them correctly. The magnifying glass actually helps in that regard.
A common scientific "toy" that is available in many stores is a "bug box". This is so-named because it has a plastic box that small objects, presumably bugs, can be put into and features a lens formed into the lid. One is sketched here:
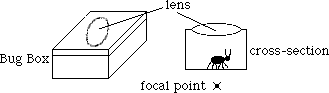
It is obvious from the previous discussion that the bug needs to be inside the focal point. If the box is designed correctly, that will occur.
Once they are online, please visit the sections on microscope, telescope and camera as well as the section on vision. All are applications of lenses which occur in our daily lives.