What are the rules by which mirrors operate when light strikes them? That is our subject.
When an ordinary object is placed in front of a plane mirror, it is sending light rays out from itself in all directions, either by emission or by reflection. This is shown here:
Therefore the light rays that strike the mirror will be doing so from a wide variety of angles. What is the pattern for light's reflection and how does it depend on angle?
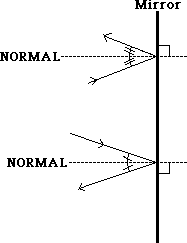
In Reflection we picture a line perpendicular to the mirror at the point of reflection. This is called the Normal. (Remember when we used the normal to define the angles in Snell's Law.) The Law of Specular Reflection states that light reflecting from a plane mirror forms an angle to the NORMAL equal to the angle between the normal and the incident light.
When an object is placed in front of a mirror, two different observers appear to see an image of the object in different places. The light, however, travels from the single object to the mirror and then to the respective observers. The manner in which it reflects must meet the conditions stated on the previously.
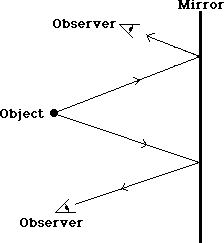
Notice how the light reflects from the smooth surface of the mirror, creating congruent or equal angles to the normal at each place it strikes the mirror. The two observers only see light when it has been reflected from the mirror in the proper manner.
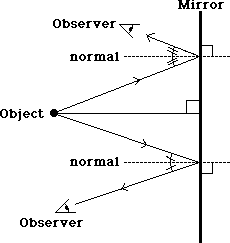
It would appear that an infinite number of images is possible for a single object. Scientists believe, however, that there should only be a single image.
What location could our two observers, or any other observers for that matter, agree upon?
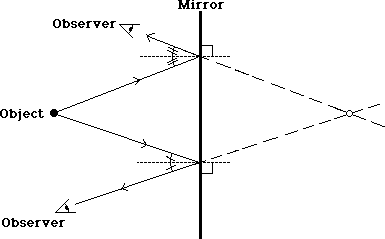
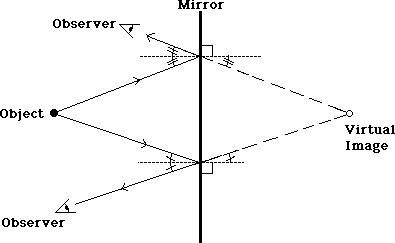
The observers' lines of sight can be extended back behind the mirror, to a place where the light rays both seem to originate. They can agree upon this one location, regardless of where they are standing. This is therefore the location of the image.
What is the nature of the light at the image location? In fact, there is no light there. This is only the apparent source of the light so it is referred to as a virtual image. Virtual images are ones that are not formed by putting the light rays together, but only appear to exist as the apparent source of the light rays.
GEOMETRY:
What is the geometry of the plane mirror's image? In the next series of drawings we can follow the geometric proof of where the image is located.
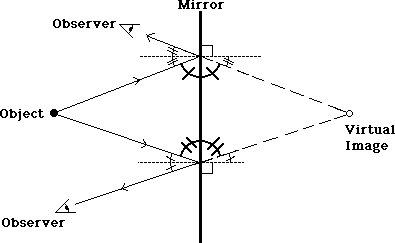
Use the vertical angle theorem to establish other angles congruent to the ones you had in the last drawing.
And use the complementary angle theorem to establish two more sets of congruent angles.
Now, using the logic of ASA, the two triangles formed, one on the object side of the mirror, the other one behind the mirror, can be proven congruent.
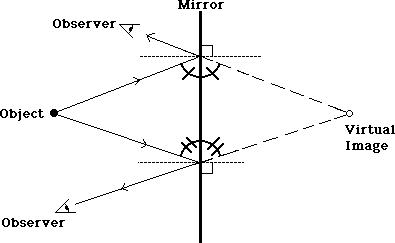
Thus the triangle "behind" the mirror is the same size and shape as the triangle in front.
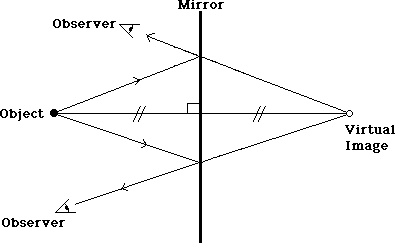
The object and its virtual image can be joined by a line which is perpendicular to the mirror, forming altitudes for the two triangles.
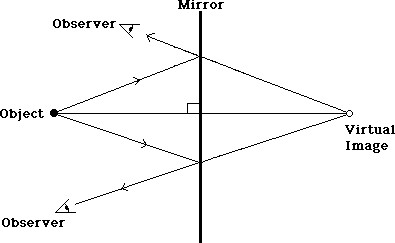
Now because the two perpendicular lines are altitudes for triangles that are exactly the same shape and size, their lengths must also be the same. This leads us to the following conclusion:
The image formed by a plane mirror will be as far behind the mirror as the object is in front of it. A line joining the two will be perpendicular to the mirror.
IMPORTANT QUESTION:
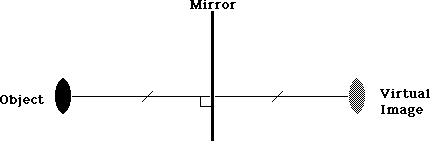
Now that we know where the image is located, we shift our attention to the size of the image. From our life experiences, we notice that our image appears to get smaller as we move away from a mirror. How else could an entire truck's image fit into the small rearview mirror on a car?
Our object (shown on the left in the diagram below) has an image which is as far behind the mirror as the object is in front. Thus the lengths of the two perpendicular lines are equal.
This equality of distance also applies at every point. In particular, we may wish to look at the line joining the "top" of the object and the "top" of the image. The line segments are equal in length and perpendicular to the mirror. The same holds true for the line segments joining the "bottom" of the object and image.
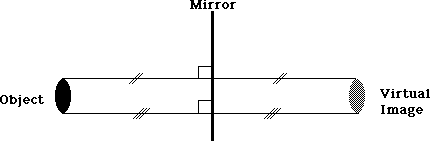
Now we look at both lines, noticing that since they are both pependicular to the mirror, they must be parallel to each other. Thus the distance from top to bottom on the object is the same as from top to bottom on the image. They're the same size!!
The image formed by a plane mirror is the same size as the object.
Why does the image look smaller, then, the further we go from a mirror? It's a simple matter of perspective. Something the same size, but further away, takes up a smaller angle of our vision. Therefore it seems to be smaller.
MORE ABOUT THE IMAGE:
A final question for thought, how is the image related to the
object? It's the same size and the same distance from the mirror.
But something's not correct. If we stand before a mirror wearing
a sweatshirt with STANFORD written on it, our image will be
wearing a sweatshirt with ![]() on it.
on it.
This brings up the nature of the image and how it's related to reality. Let's make some further observations. When we point up, does the image point up or down? It points Up, the same as we do.
If the mirror is on the north wall or your room, and you point towards the east, which direction does your image point? East, also
If you point towards the mirror (away from yourself), which direction does the image point? In the opposite direction, Towards You.
Thus, the image is reversed from front to back, not left-to-right as we are used to thinking!
Hint: The answer to the test question isn't that the image in a plane mirror is inverted, it's upright and reversed front-to-back.
Even more fascinating things happen when we employ two or more plane mirrors in combination. Check out the section on Multiple Mirrors or simply go back to the Mirror Menu or to the Main Menu.